Information numérique binaire et hexadécimale
Introduction
La connaissance du calcul binaire et hexadécimal représentent la base des compétences techniques en informatique, car toutes les informations traitées par un ordinateur sont réalisées en binaires ou en hexadécimal.
Cela permet aussi de mieux comprendre et traiter la configuration de composants d’infrastructure réseau ou de composants matériel additionnels.
La notion de base de calcul
La base représente le domaine de calcul des valeurs arithmétiques dans un système de numération donné. Par exemple en base 10, le domaine de calcul est le système décimal dans lequel le calcul arithmétique utilise les nombres de 0 à 9 c’est-à-dire 10 valeurs.
En informatique technique, on travaille sur les bases décimales, Binaires et Hexadécimales. La représentation d’un nombre dans une base s’exprime en affectant un poids à chacun des chiffres du nombre.
Un nombre peut être représenté sous la forme :
- Décimale : Un nombre comprend des chiffres de 0 à 9.
Soit une base 10 car composé de 10 chiffres différents. - Binaire : Un nombre comprend des chiffres de 0 à 1.
Soit une base 2 car composé de 2 chiffres différents. - Hexadécimale : Un nombre comprend des chiffres de 0 à 9 puis de A à F.
Soit une base 16 car composé de 16 chiffres différents.
Dans tous les cas, chaque chiffre représente une valeur dans son rang.
La somme des valeurs des chiffres de chaque rang donne la valeur totale du nombre.
La notion de valeur de rang et de poids
La position d’un chiffre dans un nombre détermine sa valeur.
Plus il y a de chiffres associés dans un nombre, plus ce nombre représente une valeur importante.
Pour symboliser ce principe, on va attribuer un rang à chacun de ces chiffres.
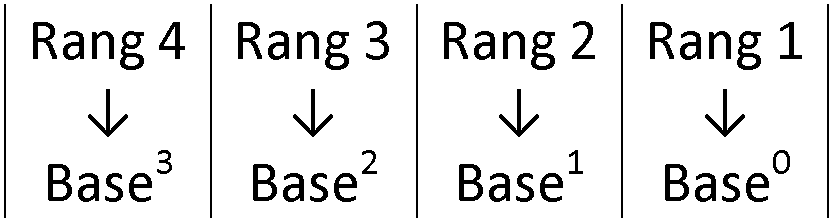
Quel que soit la base de calcul, le rang 1 exprime toujours l’unité de base.
On va donc définir 2 éléments très importants dans un code de position :
- Le rang : position d’un chiffre dans un nombre, le rang se compte en partant de la droite.
- Le poids : à chaque rang est associé un poids, c’est-à-dire le coefficient par lequel il faudra multiplier le chiffre pour obtenir sa valeur réelle.
Quel que soit la base de calcul, l’ensemble des symboles utilisés dans cette base est [0 à base-1].
La formule qui lit le poids au rang s’exprime par : Poids = Base(rang – 1)
Base 10 – le système décimal
Un nombre décimal est composé de chiffres, chaque chiffre peut prendre toute valeur comprise entre 0 et Base-1.
En base 10 un chiffre prend une valeur comprise entre 0 et (10 – 1), c’est-à-dire de 0 à 9.
Exemple de calcul sur un nombre à 4 chiffres :
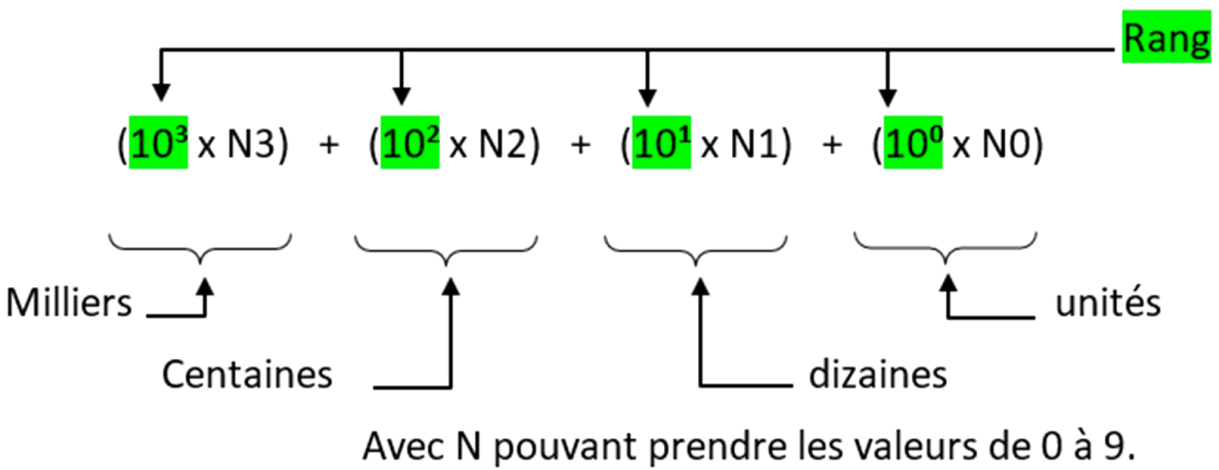
Comme vu précédemment, les puissances relatives à chaque rang sont appelées « le poids ».
Ces puissances déterminent dans quel rang se place un chiffre dans un nombre, donc le poids qu’il représente dans ce nombre.
Dans la base 10, le poids 101 exprime les dizaines, le poids 103 exprime les milliers, etc.
Le nombre 1492 est représenté par :
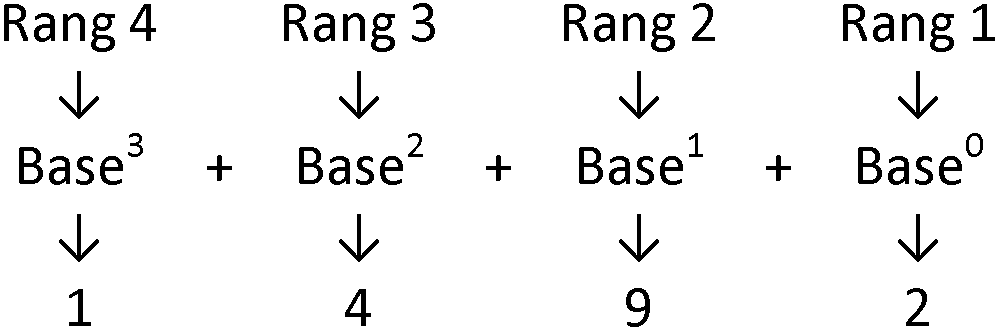
Soit en décomposition de base 10 :
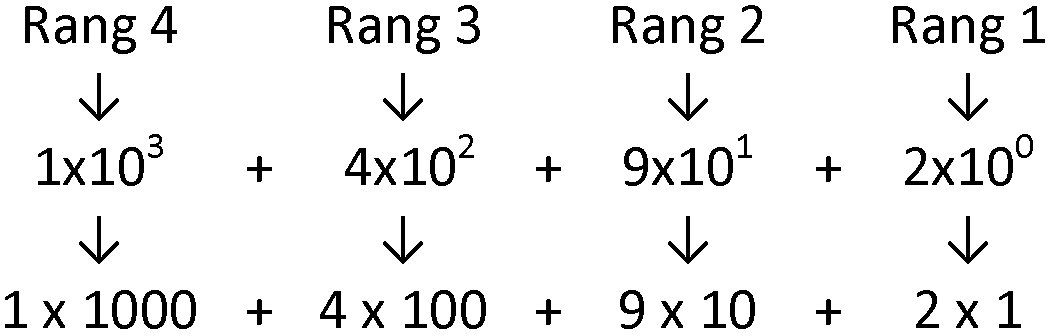
Ce qui correspond à :
1 x 1000 + 4 x 100 + 9 x 10 + 2 x 1
Pour exprimer un nombre N en base décimale, on utilise l’expression suivante : N(10)
Un nombre N en base binaire, utilise l’expression suivante : N(2)
Un nombre N en base hexadécimale, utilise l’expression : N(16)
Base 2 – le système binaire
En informatique on travaille en format binaire. C’est un concept essentiel de l’informatique. En effet, les processeurs des ordinateurs sont composés de transistors ne gérant chacun que deux états.
Le binaire ou la base 2 comporte uniquement deux symboles 0 et de 1 appelés bits pour « binary digits ».
Les composants électroniques (CPU, RAM…) manipulent des ensembles de bits sous la forme d’octets c’est-à-dire 8 éléments binaires regroupés.
On utilise le même procédé qu’en décimal ainsi une valeur binaire (ici un octet) est représentée selon la forme :
1 0 0 1 1 0 1 0
Ce qui donne
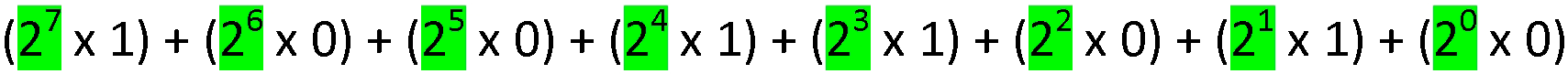
Voici les valeurs binaires des 17 premiers nombre décimaux :
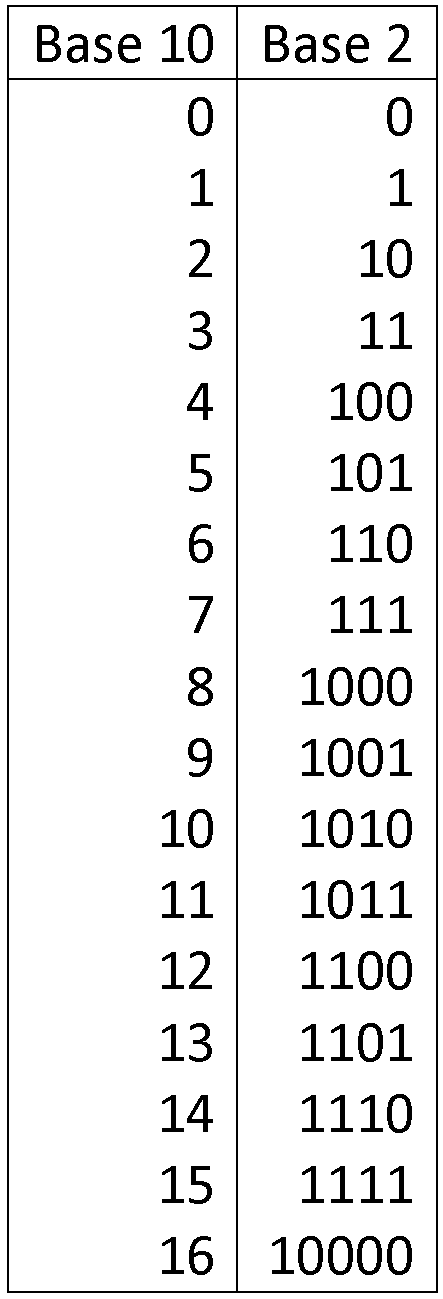
Sur le même principe que pour le système décimal, on représente le nombre 1 1 0 0 par :
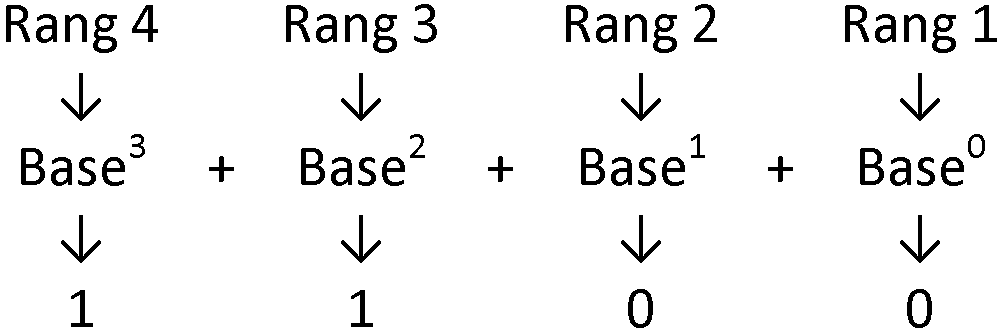
Soit en décomposition de base 2 :
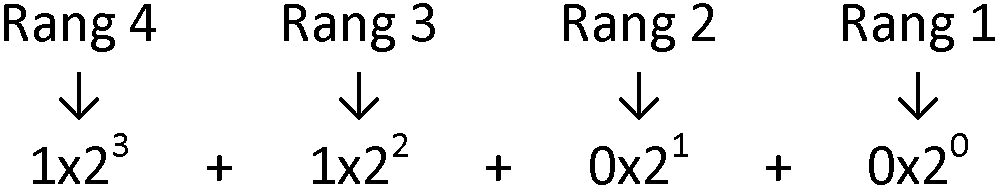
Conversion d’un nombre binaire vers un nombre décimal
Principe de la conversion :
- Dans le tableau de conversion, on place le nombre binaire en démarrant par le rang 20.
- On marque la valeur décimale de chaque colonne qui contient le chiffre 1.
- On additionne toutes les valeurs décimales marquée pour obtenir le total.
Pour convertir le nombre binaire 1 1 0 0 1 1 0 0 en décimal, il faut utiliser un tableau de conversion :
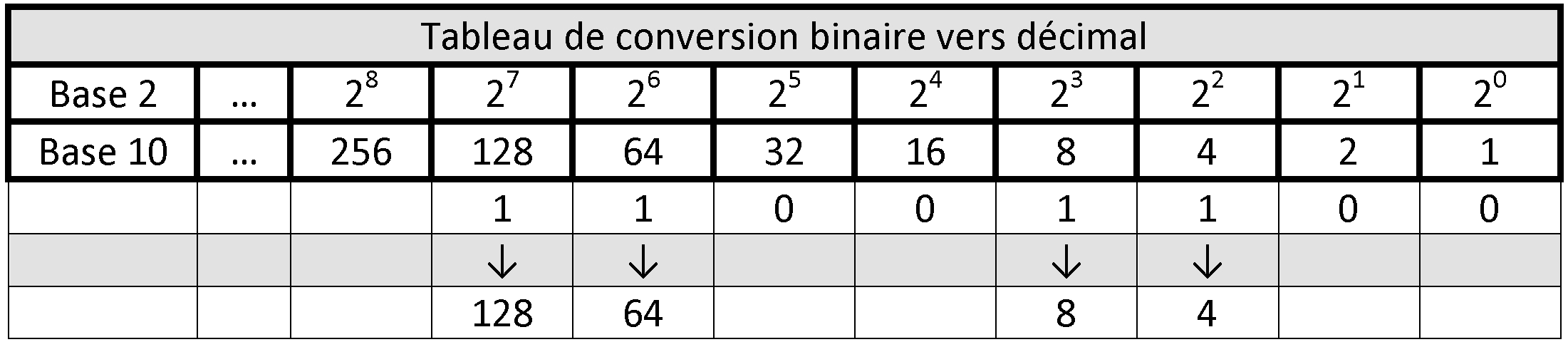
On pose le nombre binaire dans le tableau en commençant par la droite.
On note les valeurs décimales correspondant aux colonnes qui comportent des 1.
On additionne toutes les valeurs décimales obtenues :
128 + 64 + 8 + 4 = 204
Donc le nombre binaire 1 1 0 0 1 1 0 0 correspond à la valeur décimale 204.
Il reste à noter le résultat de manière lisible : 1 1 0 0 1 1 0 0(2) = 204(10)
Exemple de conversion du nombre 1 1 1 1 1 1 1 1 :
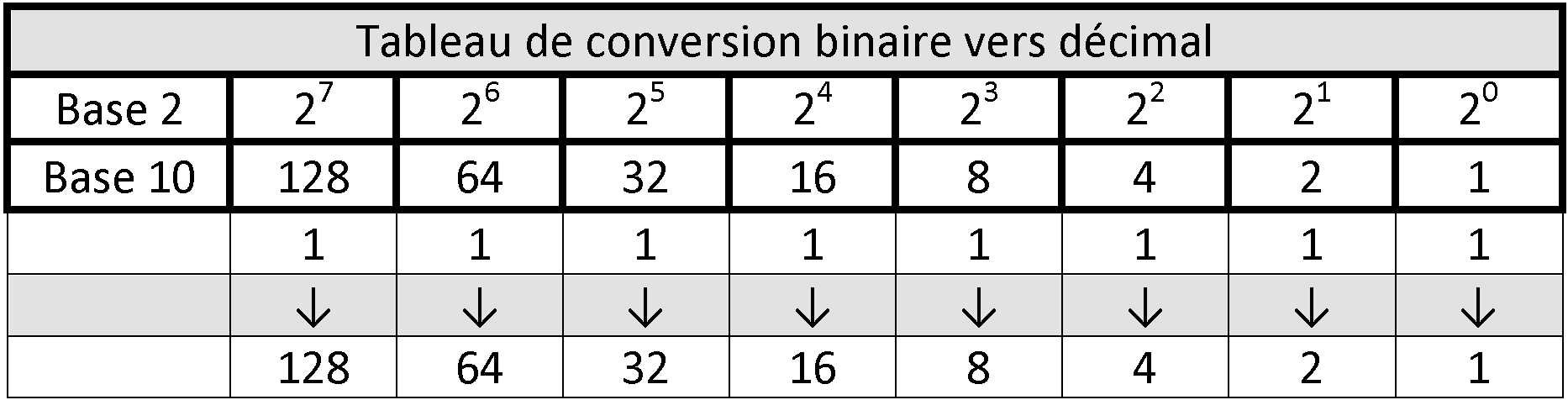
Soit la somme 128 + 64 + 32 + 16 + 8 + 4 + 2 + 1 = 255.
Donc le nombre binaire 1 1 1 1 1 1 1 1 correspond à la valeur décimale 255.
On note le résultat : 1 1 1 1 1 1 1 1(2) = 255(10)
Conversion d’un nombre décimal vers un nombre binaire par soustraction
Principe de la conversion :
- Dans le tableau, on situe le nombre décimal le plus proche du nombre à convertir, sans le dépasser.
- On place 1 dans la colonne correspondant au poids.
- On soustrait du nombre à convertir la valeur positionnée dans la colonne.
- On réitère l’opération avec le résultat de la soustraction jusqu’à obtenir un reste égal à 0.
- On complète par des zéros les poids non positionnés.
Pour convertir le nombre décimal 233 en binaire, il faut utiliser le tableau de conversion.
Mais la méthode est très différente !
On repère dans le tableau le nombre décimal qui se rapproche le plus de 233 mais qui ne dépasse pas sa valeur.
Donc le nombre 128.
On note un chiffre 1 dans la colonne 27.
Puis on soustrait la valeur 128 au nombre 233. 233 – 128 = 105
On repère ensuite dans le tableau le nombre décimal qui se rapproche le plus de 105 mais qui ne dépasse pas.
Donc le nombre 64.
On note un chiffre 1 dans la colonne 26.
Puis on soustrait la valeur 64 au nombre 105. 105 – 64 = 41
On repère ensuite dans le tableau le nombre décimal qui se rapproche le plus de 41 mais qui ne dépasse pas.
Donc le nombre 32.
On note un chiffre 1 dans la colonne 25.
Puis on soustrait la valeur32 au nombre 41. 41 – 32 = 9
On repère ensuite dans le tableau le nombre décimal qui se rapproche le plus de 9 mais qui ne dépasse pas.
Donc le nombre 8.
On note un chiffre 1 dans la colonne 23.
Puis on soustrait la valeur 8 au nombre 9. 9 – 8 = 1
On repère ensuite dans le tableau le nombre décimal qui se rapproche le plus de 1 mais qui ne dépasse pas.
Donc le nombre 1.
On note un chiffre 1 dans la colonne 20.
Puis on soustrait la valeur 1 au nombre 1. 1 – 1 = 0
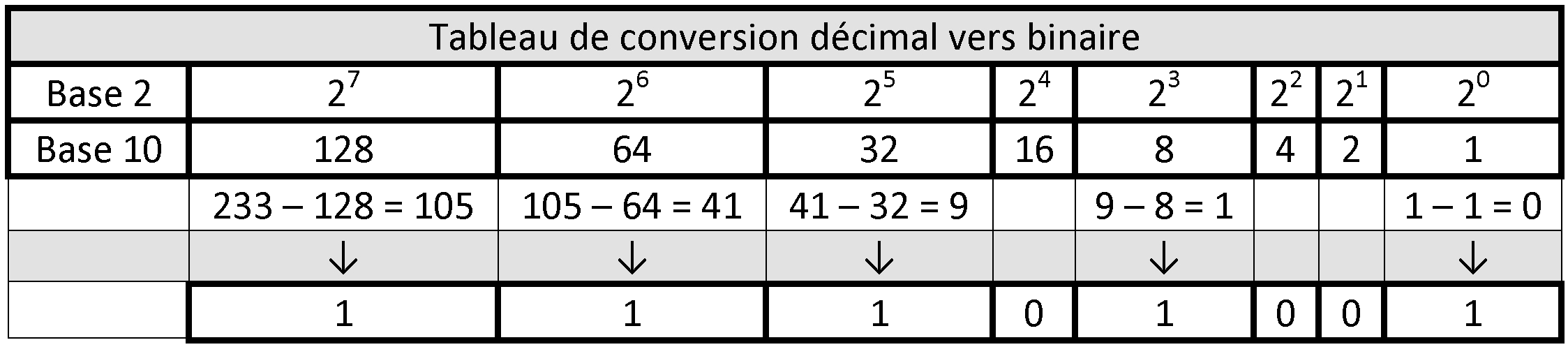
Il ne reste plus qu’à compléter les espaces vides par des 0 pour obtenir le nombre binaire final :
1 1 1 0 1 0 0 1
On obtient le résultat : 233(10) = 1 1 1 0 1 0 0 1(2)
Conversion d’un nombre décimal vers un nombre binaire par division
Principe de la conversion :
- On divise le nombre décimal par 2 et on conserve le reste de la division, qui sera 1 ou 0.
- On divise le quotient obtenu par 2 et on conserve le reste de la division, qui sera 1 ou 0.
- On réitère l’opération à partir du quotient jusqu’à ce que le quotient soit nul.
- On note les résultats des restes des divisions en inversant leur ordre.
Cela revient à calculer les modulos 2 du nombre.
Un modulo est le reste de la division entière entre 2 nombres.
Exemple avec le nombre décimal 57(10) :
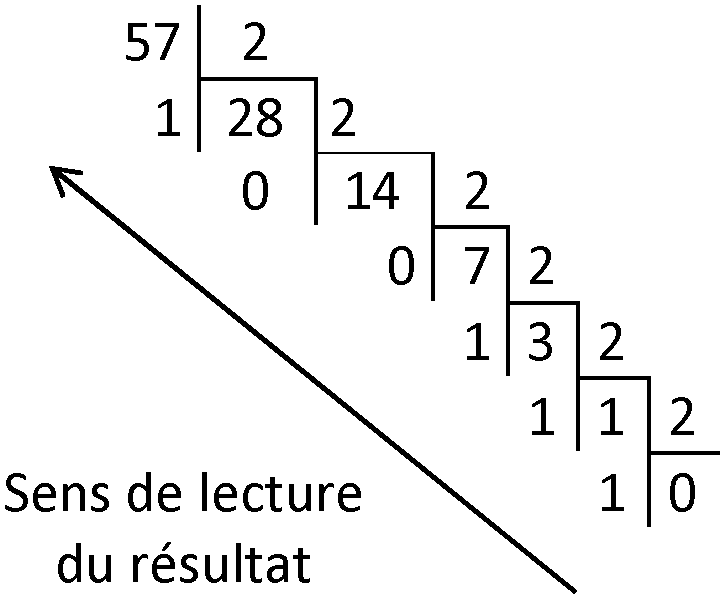
57/2 = 28 il reste 1, car 57 = 2 x 28 + 1
28/2 = 14 il reste 0, car 28 = 2 x 14
14/2 = 7 il reste 0, car 14 = 2 x 7
7/2 = 3 il reste 1, car 7 = 2 x 3 + 1
3/2 = 1 il reste 1, car 3 = 2 x 1 + 1
1/2 = 0 il reste 1, car le résultat de la division n’est pas égal à 0
Arrêt de l’opération car le quotient est égal à 0
On rassemble tous les restes dans le sens inverse de leur obtention : 1 1 1 0 0 1
On obtient donc le résultat : 57(10) = 1 1 1 0 0 1(2)
Conversion rapide d’un nombre décimal vers un nombre binaire
Dans certains cas spécifiques, on peut rapidement déduire la valeur binaire d’une valeur décimale.
Exemple pour le nombre 223.
Par expérience, on sait que le nombre décimal 255 a la valeur binaire 1 1 1 1 1 1 1 1.
Si on soustrait 223 à 255 on trouve la valeur 32.
(255 – 223 = 32)
Lorsque l’on regarde le tableau de conversion, on constate que la valeur 32 est une valeur spécifique de ce tableau qui correspond à la colonne 25.
Donc on peut tout simplement remplacer la valeur 1 de la colonne 25 par un 0 pour faire la soustraction de cette valeur.

On déduit donc très rapidement que le nombre décimal 223 équivaut au nombre binaire :
1 1 0 1 1 1 1 1
Base 16 – le système hexadécimal
La représentation hexadécimale est la base 16 dont la représentation numérique est la suivante :
On utilise les 10 chiffres décimaux 0 à 9 puis les caractères A (pour 10), B (pour 11), C (pour 12), D (pour 13), E (pour 14) et F (pour 15) afin de réaliser les seize valeurs de la base.
Sur le même principe que pour le système décimal et le système binaire, on représente le nombre 4 C 0 A par :
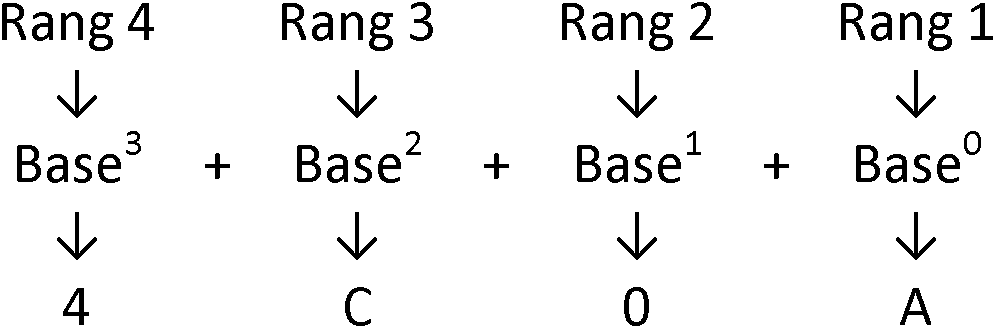
Soit en décomposition de base 16 :
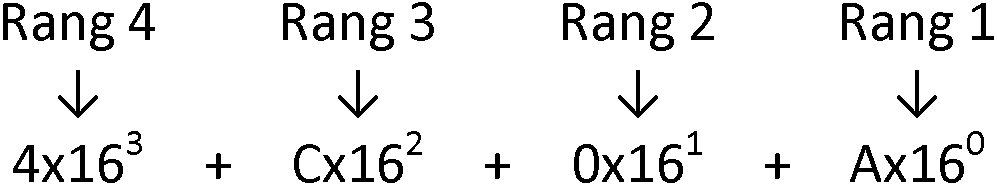
Voici les valeurs hexadécimales des 17 premiers nombre décimaux :
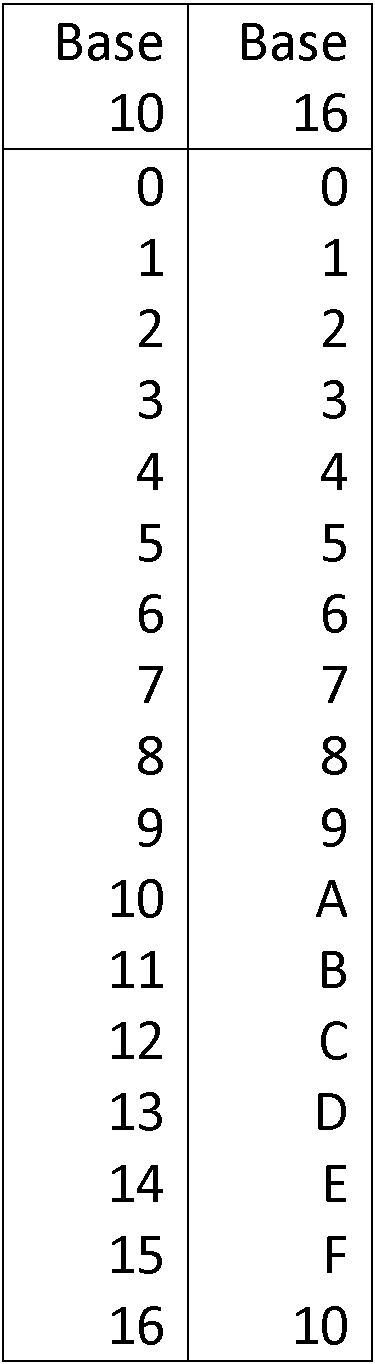
Conversion d’un nombre hexadécimal vers un nombre décimal
Principe de la conversion :
- On transforme toutes les lettres hexadécimales en son équivalent décimal.
- On multiplie chaque chiffre hexadécimal avec le poids qu’il représente.
- On fait la somme de tous les résultats obtenus.
Comme dans toute base, un chiffre possède la valeur du rang dans lequel il se trouve, c’est son poids. Le 1er chiffre à droite est l’unité dont sa valeur est égale au chiffre multiplié par 160. Le 2ème chiffre possède une valeur multipliée par 161. Le 3ème possède une valeur multipliée par 162, etc.
Pour convertir en décimal une valeur hexadécimale, on multiplie chaque chiffre hexadécimal par la puissance de 16 correspondant au rang dans lequel se trouve le chiffre. Pour les chiffres allant de A à F, il faudra préalablement les convertir à leur valeur décimale associée (C = 12, F = 15, etc.).
Dans l’exemple ci-dessus avec le nombre hexadécimal 825 on aura :
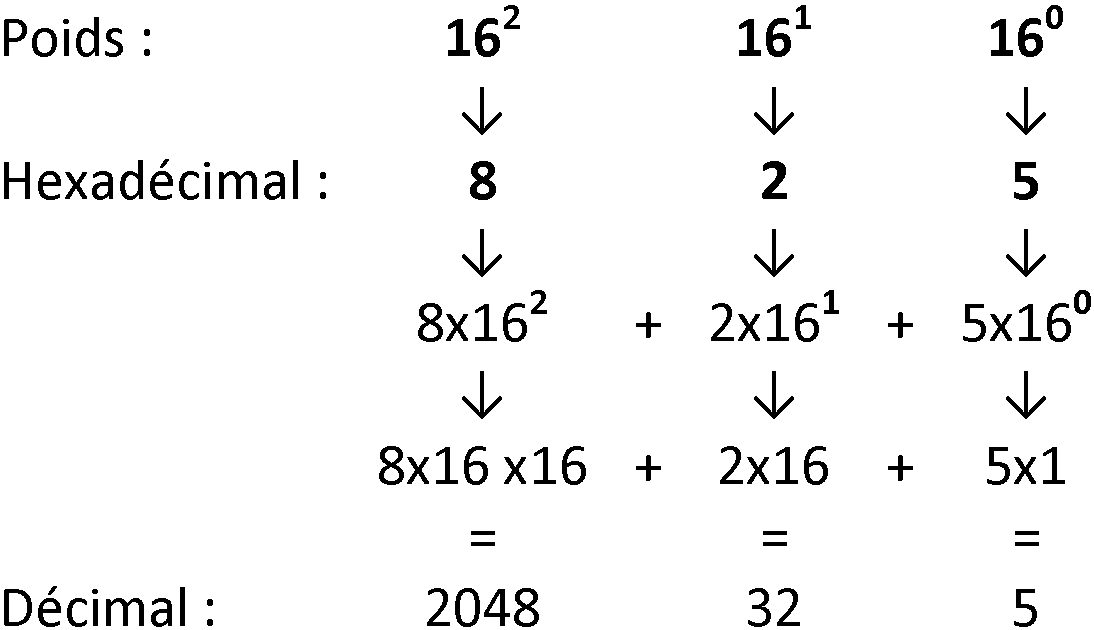
Ce qui donne : 2048+32+5 = 2085
Donc le résultat de valeurs 825(16) = 2085(10)
Soit par exemple une représentation à 4 chiffres sous la forme 4C0A, on a alors :
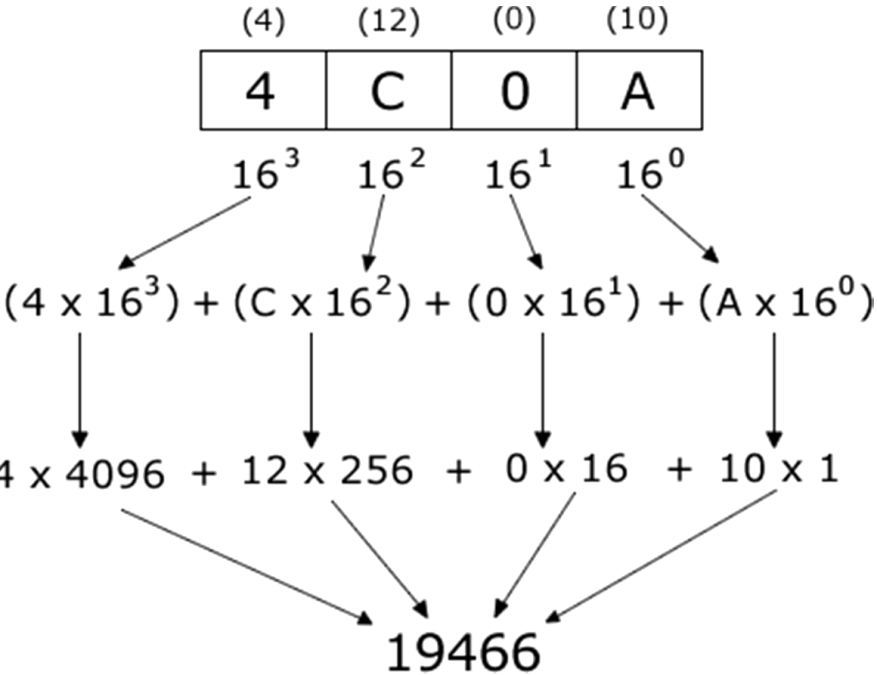
Donc le résultat de 4C0A(16) = 19466(10)
Conversion d’un nombre hexadécimal vers un nombre binaire
Principe de la conversion :
- On transforme toutes les lettres hexadécimales en son équivalent décimal.
- On convertit chaque chiffre hexadécimal en binaire sur 4 octets.
- On assemble chaque valeur binaire à la suite, selon l’ordre naturel d’écriture.
Pour convertir le nombre hexadécimal DE1A en binaire, il faut simplement décomposer chaque chiffre par leur équivalent décimal, puis convertir chaque chiffre en binaire en les notant toujours sur 4 octets :
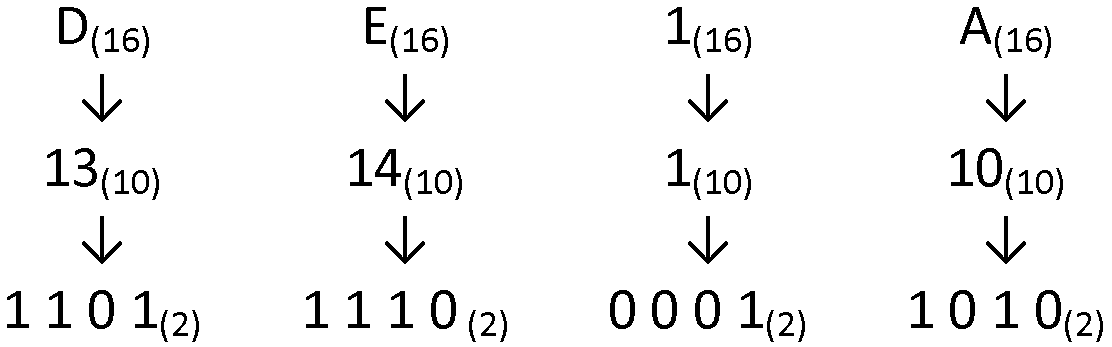
Ensuite on rassemble les valeurs les unes à la suite des autres dans l’ordre d’écriture :

Donc le résultat de la valeur DE1A(16) = 1 1 0 1 1 1 1 0 0 0 0 1 1 0 1 0(2)
Conversion d’un nombre décimal vers un nombre hexadécimal
Principe de la conversion :
- On divise le nombre décimal par 16 et on conserve le reste de la division qui sera inférieur à 16.
- On divise le quotient obtenu par 16 et on conserve le reste de la division qui sera inférieur à 16.
- On réitère l’opération à partir du quotient jusqu’à ce que le quotient soit inférieur à 16.
- On note les résultats de tous les restes des divisions en inversant leur ordre.
La conversion décimale vers hexadécimal est le processus inverse de celui de la conversion hexadécimale vers le décimal.
Cette conversion s’obtient par division successive par 16 du nombre décimal.
Pour convertir le nombre décimal 2590, il faut utiliser la méthode modulo.
Donc on utilise la division Euclidienne par 16.
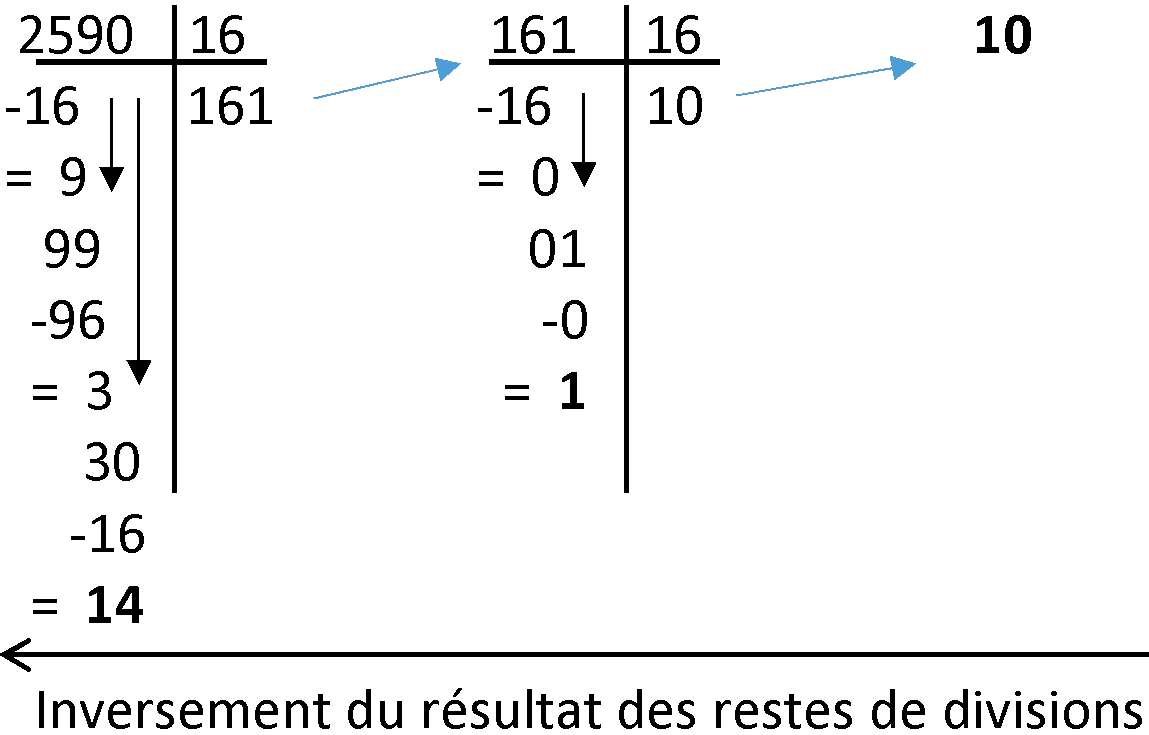
On divise le nombre 2590 par 16, jusqu’à arriver au reste qui est inférieur à 16 et on note le reste qui est 14.
Puis on divise le quotient, (résultat de la division) 161 par 16, jusqu’à arriver au reste 1 et on le note.
On continue jusqu’à ce que le quotient soit inférieur à 16 et on note le quotient.
Il faut ensuite convertir toutes les valeurs supérieures à 9 en valeurs hexadécimales :
A = 10 ; B = 11 ; C = 12 ; D = 13 ; E = 14 ; F = 15
Pour terminer, on inverse le sens d’écriture des restes obtenus dans les divisions :
A (10), 1, E (14)
Donc le nombre décimal 2590 correspond au nombre hexadécimal A1E.
Il reste à noter le résultat de manière lisible : 2590(10) = A1E(16)