Les nombres entiers signés / non signés
En informatique les caractères sont représentés sous forme binaire dans lequel un caractère est définit par un octet (256 codes possibles).
Les nombres sont présentés sous la forme d’entiers naturels ou d’entiers relatifs.
Un entier naturel est un entier positif ou nul. Un entier relatif est un entier positif, négatif ou nul. Pour représenter un nombre relatif, 2 formes de codage sont possibles :
- un entier relatif positif ou nul sera représenté en binaire (base 2) comme un entier naturel, à la seule différence que le bit de poids fort (le bit situé à l’extrême gauche) représente le signe. Il faut donc s’assurer pour un entier positif ou nul qu’il est à zéro (0 correspond à un signe positif, 1 à un signe négatif). Ainsi si on code un entier naturel sur 4 bits, le nombre le plus grand sera 0111 (c’est-à-dire 7 en base décimale).
D’une manière générale le plus grand entier relatif positif codé sur n bits sera 2^n-1-1.
- un entier relatif négatif grâce au codage en complément à deux.
Principe du complément à deux :
Soit à représenter un nombre négatif.
-
- Prenons son opposé (son équivalent en positif)
- On le représente en base 2 sur n-1 bits
- On complémente chaque bit (on inverse, c’est-à-dire que l’on remplace les zéros par des 1 et vice-versa)
- On ajoute 1
Voyons maintenant cela sur un exemple :
On désire coder la valeur -5 sur 8 bits. Il suffit :
- d’écrire 5 en binaire 0 0 0 0 0 1 0 1
- de complémenter à 1 1 1 1 1 1 0 1 0
- d’ajouter 1 1 1 1 1 1 0 1 1
- la représentation binaire de -5 sur 8 bits est : 1 1 1 1 1 0 1 1
Nombres binaires avec une virgule
Les nombres réels décimaux
Les nombres réels décimaux sont des nombres non entiers représentés avec une virgule. Deux parties sont présentes dans un nombre à virgule :
Chiffres situés à gauche de la virgule : la partie entière
Chiffres situés à droite la virgule : la partie fractionnaire
Par exemple :
21,9 21 est la partie entière et 9 est la partie fractionnaire
On convertit un nombre décimal à virgule en base 2 (par exemple : 189,32 en effectuant 2 opérations :
Conversion binaire de la parie entière (dans cet exemple : 1 0 1 1 1 1 0 1 = 189)
N multiplications successive par 2 de la partie fractionnaire (N définit la précision du calcul de la partie fractionnaire. Plus N est grand plus la précision est importante)
Ainsi (avec N codé sur 4 bits) :
0,32 * 2 = 0,64
0,64 * 2 = 1,28
0,28 * 2 = 0,56
0,56 * 2 = 1.12
N = 0 1 0 1 Le nombre est donc 1 0 1 1 1 1 0 1 , 0 1 0 1
3.1.2 Les réels (flottants)
Un nombre réel est composé d’une partie entière et d’une partie fractionnaire.
1ère méthode : par multiplication successive de la partie réelle
On convertit séparément les parties entière et fractionnaire :
- Partie entière (Déjà vue plus haut)
- Partie fractionnaire :
On multiplie par 2 le nombre fractionnaire :
- s’il y a retenue, alors on note 1, sinon, on note 0,
- et ce, jusqu’à ce que la partie fractionnaire, soit nulle ou infinie.
Exemple : 4,625(10) = x(2)
Rappel : 4,625(10) = 4×100 + 6×10-1 + 2×10-2 + 5×10-3
- Partie entière : 4(10) =100(2)
Partie fractionnaire : 0,625 =
On multiplie la partie fractionnaire par 2.
Soit le résultat obtenu contient une partie entière (au-dessus de la virgule), alors on note 1, sinon on note 0.
Ensuite on continue avec la partie fractionnaire obtenue et on multiplie à nouveau par 2.
Jusqu’à ce que la partie fractionnaire soit égale à 0.
0,625 x 2 = 1,250 on note 1
0,250 x 2 = 0,500 on note 0
0,500 x 2 = 1,000 on note 1
Arrêt car la partie fractionnaire = 0
4,625(10) = 100,101(2)
2ème méthode : par transformation d’un nombre réel en nombre entier
- on multiplie le nombre réel par 2 autant de fois que nécessaire pour obtenir un nombre entier,
- on recherche le code binaire de ce nombre entier,
- on place la virgule en la décalant vers la gauche d’autant de fois qu’on avait multiplié par 2.
Exemple : 4,625(10) = x(2)
Transformation du nombre réel en nombre entier :
4,625 x 2 = 9,25
9,25 x 2= 18,7
18,5 x 2= 37
Conversion du nombre entier en binaire :
37(10) = 100101(2)
Placement de la virgule : Le nombre a été multiplié 3 fois par 2 ; on place la virgule après le 3ème nombre en comptant à partir de la droite :
4,625(10) = 100,101(2)
3ème méthode : par soustraction de la partie fractionnaire
4,625(10) = x(10)
- Partie entière :
4(10) =100(2)
- Partie fractionnaire : 0,625(10)
- Dans 0,625 il y a 0,50 on note 1. Il reste à placer 0,625-0,50=0,125
- Dans 0,125 il n’y a pas 0,25. On note 0
- Dans 0,125 il y a 0,125 on note 1. Il reste à placer 0,125-0.125=0
Donc 0,625(10) = 0,101(2)
4,625(10) = 100,101(2)
L’addition binaire
Le calcul binaire est utilisé en électronique logique et en informatique et plus particulièrement en réseau pour les opérations binaires sur les adresses physiques et logiques appliquées aux machines.
Le calcul binaire utilise les opérations arithmétiques (addition, soustraction, multiplication, division) et logiques pour tous les traitements informatiques.
| Calcul d’une addition en décimal : |
+ | 1 9 —- 10 |
Calcul d’une addition en binaire : |
+ | 1 1 —- 10 |
Dans le calcul décimal on passe au rang suivant (les dizaines par exemple) quand on dépasse la valeur maximale du rang en cours, soit le dépassement de 9.
Dans le calcul binaire, c’est exactement le même principe mais il intervient dès que la valeur de 1 est dépassée.
Exemples de calcul d’une addition de 2 nombres binaires :
| +1 +1 | +1 +1 +1 +1 +1 +1 +1 +1 +1 | |||
| ↓ ↓ | ↓ ↓ ↓ ↓ ↓ ↓ ↓ ↓ | |||
| 1 0 1 0 0 1 1 0 | 1 1 1 1 1 1 1 1 | |||
| + | 0 1 0 1 0 1 1 1 | + | 1 1 1 1 1 1 1 1 | |
| —————— | ———————- | |||
| 0 0 0 0 0 1 1 0 | 1 1 1 1 1 1 1 1 1 |
Les opérateurs logiques binaires
L’algèbre de Boole permet de définir les lois binaires logiques :
« ET », « OU », « NON », « OU exclusif », etc…
On considère 2 valeurs d’entrée A et B, chacune des entrées peut prendre 2 valeurs. On calcule la résultante en sortie des fonctions logiques Et, OU, OU Exclusif et NON en fonction des valeurs que prennent chaque entrée.
| A | B | ET | OU | OU Exclu. | NON ET | NON OU |
| 0 | 0 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 0 | 0 | 0 |
En informatique technique, on utilisera principalement les opérateurs « ET » et « OU ».
Voici un schéma d’un composant avec l’opération « ET » ou « OU » :

En considérant que le composant possède 2 entrées, alors selon que sa fonction soit « ET » ou « OU » la valeur de sortie sera différente.
Voici le tableau des différentes solutions possibles selon la valeur binaire qui sera proposée dans les entrées E1 et E2 et l’opérateur logique qui traitera ces entrées :
| Entrée E1 | Entrée E2 | Sortie « OU » | Sortie « ET » |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 1 |
La fonction « OU » renvoie 1 si une des entrées est alimentée.
La fonction « ET » renvoie 1 uniquement si toutes les entrées sont alimentées.
Exemples de calcul d’une opération logique « OU » de 2 nombres binaires :
| 1 0 1 0 0 1 1 0 | 1 0 1 0 1 0 1 0 | |||
| OU | 0 1 0 1 0 1 1 1 | OU | 0 1 0 1 0 1 0 1 | |
| —————— | —————— | |||
| 1 1 1 1 0 1 1 1 | 1 1 1 1 1 1 1 1 |
S’active si une des valeurs est 1, sinon le résultat est 0.
Exemples de calcul d’une opération logique « ET » de 2 nombres binaires :
| 1 0 1 0 0 1 1 0 | 1 0 1 0 1 0 1 0 | |||
| ET | 0 1 0 1 0 1 1 1 | ET | 0 1 0 1 0 1 0 1 | |
| —————— | —————— | |||
| 0 0 0 0 0 1 1 0 | 0 0 0 0 0 0 0 0 |
S’active uniquement si les 2 valeurs sont 1, sinon le résultat est 0.
Tableau de Karhaugh (table de vérité)
La table de vérité permet de déterminer toutes les valeurs possibles d’une combinaison de n bits qui ne prennent que 2 valeurs 0 ou 1.
On passe d’un nombre binaire au suivant en ajoutant 1, comme en décimal, sans oublier les retenues avec la loi suivante :
0+0=0 ; 0+1=1 ; 1+0=1 ; 1+1=10
En logique binaire, 1 + 1 = 0 avec retenue de 1 vers la gauche, ainsi :
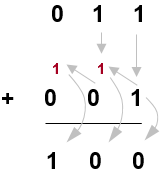
0 1 1 + 0 0 1 = 1 0 0
Par exemple faire la somme des nombres 1 0 1 1 0 1 + 1 0 1 0 revient à additionner 1 0 1 1 0 1 à 0 0 1 0 1 0, c’est-à-dire
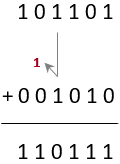
Soit à additionner les 2 nombres binaires : 1011 et 0101.
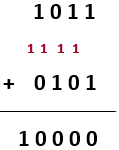
La multiplication est apparentée à la fonction ET logique. Ainsi pour ces 2 opérations, on obtient le tableau suivant.
| A | B | Multiplication (A x B) | Addition (A + B) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 10 |
La table de vérité en logique binaire
Ci-dessous la table de vérité pour un ensemble de 4 entrées A, B, C et D soit 24 possibilités. Ces valeurs sont obtenues par addition successive.
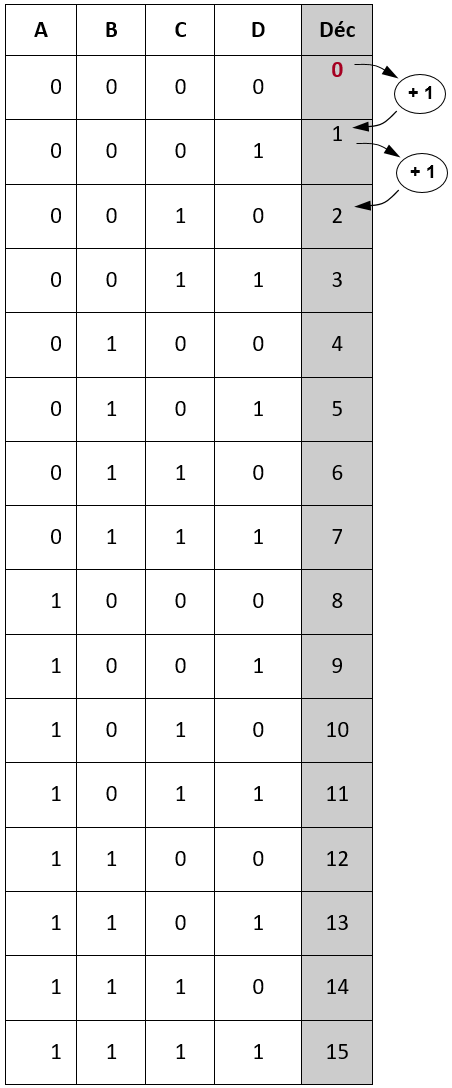
Représentation à virgule flottante
Pour pouvoir représenter les nombres positifs et négatifs, il faut réserver le premier bit pour indiquer le signe. En mode 16 bits on ne peut représenter que les nombres compris entre +32767 et -32767. Si on veut coder des nombres plus grands on passe aux nombres en virgule flottante.
C’est la notation utilisée sur les calculettes :
| 300 000 = 0,3 106
0,3 est la mantisse 6 est l’exposant
|
||
| Exemples | ||
| 65,1234 | = 0,651 102 | = 0,651 E2 |
| 0,00034 | = 0,340 10-3 | = 0,340 E-3 |
| – 512 | = – 0,512 103 | = – 0,512 E3 |
Codage :
- De manière évidente, il va nous falloir des bits pour coder la mantisse
- Et un autre groupe de bits pour coder l’exposant
Format en simple précision (sur 32 bits) :
| 31 | 30 | 23 | 22 | 0 | |||
| Signe | Exposant | Mantisse | |||||
| 1 bit | 8 bits | 23 bits | |||||
Format en double précision (sur 64 bits) :
| 63 | 62 | 52 | 51 | 0 | |||
| Signe | Exposant | Mantisse | |||||
| 1 bit | 11 bits | 52 bits | |||||
Nous désirons stocker des données dans une machine. Ainsi le nombre 9,750 se trouvera mémorisé sous la forme suivante :
1 0 0 1 1 1 (avec les 2 derniers 1 = résultat de la conversion binaire de 0,750)
Toutefois cette expression binaire ne suffit pas à définir totalement notre donnée car il n’y a aucune indication sur la valeur du poids binaire affecté aux différents bits, d’où la notion suivante de virgule :
1 0 0 1 , 1 1
En utilisant cette notion de virgule, notre nombre peut s’écrire de la manière ci-après :
N = 0 1 0 0 1 , 1 1 x 20
N = 0 1 0 0 , 1 1 1 x 21
N = 0 1 0 , 0 1 1 1 x 22
N = 0 1 , 0 0 1 1 1 x 23
N = 0 , 1 0 0 1 1 1 x 24
La dernière expression présente l’avantage de représenter la grandeur par un nombre inférieur à 1 multiplié par une puissance de 2.
L’exposant 4 est bien entendu représentatif de la position de la virgule (ici : 100).
Le terme 1 0 0 1 1 1 appelé Mantisse (M),
Le terme 1 0 0 appelé Exposant (E)
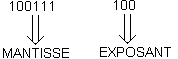
On retrouve ainsi le même nombre sous deux formes différentes :
N = 1 0 0 1 1 1 x 24
N = 1 0 0 1 , 1 1
Codage ASCII, BCD
Ces lois permettent de coder en binaire les valeurs numérique et alphanumériques.
L’ASCII définit 128 caractères numérotés de 0 à 127 et codés en binaire de 0000000 à 1111111. Sept bits suffisent donc pour représenter un caractère codé en ASCII. Toutefois, les ordinateurs travaillant presque tous sur huit bits (un octet) depuis les années 1970, chaque caractère d’un texte en ASCII est stocké dans un octet dont le 8e bit est 0.
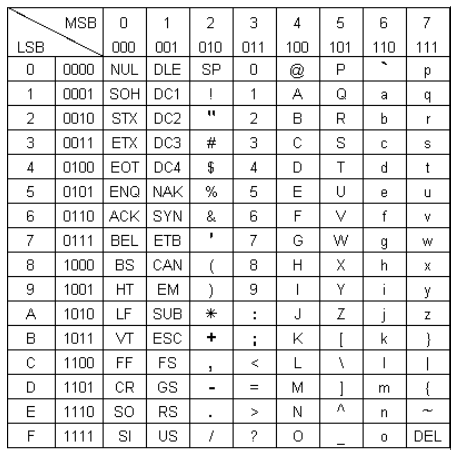
Le codage BCD permet de coder en binaire chacun des chiffres qui composent un nombre. Un chiffre décimal est codé sur 4 bits. Par exemple si l’on veut coder le nombre décimal 1997, on obtient :
1 9 9 7
0001 1001 1001 0111
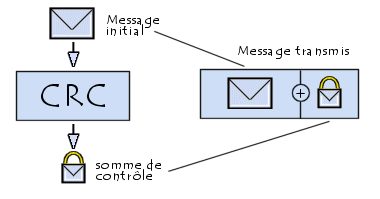
Codes détecteurs d’erreur CRC
On n’étudiera ici que les codes détecteurs de type CRC (code à redondance cyclique). En informatique, un contrôle de redondance cyclique ou CRC (Cyclic Redundancy Check) est un outil permettant de détecter les erreurs de transmission pouvant intervenir sur les lignes de transmission réseau ou télécom.
Les CRC sont calculés avant et après la transmission, puis comparés pour s’assurer que ce sont les mêmes. Les calculs de CRC les plus utilisés sont construits de manière à ce que les erreurs de certains types, comme celles dues aux interférences dans les transmissions, soient toujours détectées.
Le principe du CRC consiste à traiter les séquences binaires comme des polynômes binaires, c’est-à-dire des polynômes dont les coefficients correspondent à la séquence binaire. Ainsi la séquence binaire 0110101001 peut être représentée sous la forme polynomiale suivante :
0*X9 + 1*X8 + 1*X7 + 0*X6 + 1*X5 + 0*X4 + 1*X3 + 0*X2 + 0*X1 + 1*X0
soit
X8 + X7 + X5 + X3 + X0
ou encore
X8 + X7 + X5 + X3 + 1
De cette façon, le bit de poids faible de la séquence (le bit le plus à droite) représente le degré 0 du polynôme (X0 = 1), le 4ème bit en partant de la droite représente le degré 3 du polynôme (X3)… Une séquence de n bits constitue donc un polynôme de degré maximal n-1.
Dans ce mécanisme de détection d’erreur, un polynôme prédéfini (appelé polynôme générateur et noté G(X)) est connu de l’émetteur et du récepteur.
La détection d’erreur consiste pour l’émetteur à effectuer un algorithme sur les bits de la trame afin de générer un CRC, et de transmettre ces deux éléments au récepteur. Il suffit alors pour le récepteur d’effectuer le même calcul afin de vérifier si le CRC est valide.